The College Board rolled out the new Digital SAT in the United States in March of this year; the next administration is right around the corner at the beginning of October. Putting together what we’ve seen on the new practice tests and what we’ve heard from our students who have taken the test, it’s safe to say that the math on this test can be hard.
In this post, we’ll delve into some problems that illustrate the ways in which the hardest math questions on this revised test are challenging and what to do to approach them successfully. We’ll illustrate a variety of ways to tackle these problems, noting some rather extreme differences in time and difficulty, and drawing some lessons for navigating these monster questions quickly and accurately.
The Digital SAT and Difficult Quadratics
A first observation is that, whereas the ACT tests a broad range of math topics, the SAT tends to go deep on a handful of topics, especially quadratics (you’ll also want to be handy with the equation for a circle). Here are some things you might want to brush up on:
- standard form y = ax2 + bx + c
- vertex form y = a(x – h)2 + k (h, k) = vertex
- discriminant b2 – 4ac
- and its relation to number of solutions: d > 0: 2 solns, d = 0: 1 soln, d < 0: no real solutions
- what it means, graphically, for a quadratic to have two, one, or zero real solutions
- completing the square
- connection between factors of the equation and its zeroes
vertex is at: x-value = –b/2a, halfway between its zeroes (if any) - how to use Desmos to “adjust” your curves
That said, the hardest quadratics problems require a mix of skills deployed together, and the mental flexibility and big-picture understanding to reason about cases where, say, coefficients in the quadratic equation are left as variables, or you have to supply a minimal or maximal value that will make the equation have no real solutions, etc.
Problem Solving and Quantitative Reasoning on the SAT: Make it Tangible!
The central goal throughout is one that we emphasize for all mathematics problems: make it more tangible! Things are hard when they are abstract and unfamiliar, while people are fast and accurate in reasoning about things and situations they’re familiar with.
To give a simple example: calculate in your head, as quickly as you can, what 9 x 25 is. Some people can do this effortlessly; others are slower. But pretty much everyone is quicker and more accurate in answering the very same question phrased a different way: you find 9 quarters; how much money do you have? …$2.25, obviously. It’s the same math, but whether it’s presented as something you deal with every day, or as something more abstract, makes a world of difference.
So then, let’s take our own advice and go from high-level description to actual questions…
How to Tackle the Most Difficult Digital SAT Math Questions: Example 1

And, here we go: a wildly abstract question about a quadratic where several of the coefficients are left as variables. Notice that is question 22 (out of 22); questions this hard will cluster at the end of the section.
The first lesson is to not get overwhelmed by a question like this: it is initially intimidating, and basically no one sees their way through it right away. The key is to keep your wits about you and an eye on the bigger picture, trust what you know, and be scrappy. So buck up, and let’s dive in!
Ok, let’s see what we can do with this. One way through is to try to use reasoning and algebra. This is doable, but difficult. We’ll walk through it, just to illustrate what’s involved.
We’re told that the parabola opens upward: this tells us that a > 0. Unfortunately, that doesn’t tell us whether a ≥ 1, the question at issue in (II).
What else do we know? The statement f(–9) = f(3) is really important. A parabola is symmetric about a vertical line through its vertex, so these x-values have to be the same distance from the vertex. That puts the vertex at an x-value of –3, halfway between –9 and 3.
Now for some algebraic knowledge: the x-coordinate of the vertex h is equal to –b/2a (if you know the quadratic equation, you can see that –b/2a is the central point which you’re adding to and subtracting from). Now we’re getting somewhere! Since we know the final value (it’s –3), and b, we can solve for a.
x-coordinate of vertex = –b/2a
–3 = –(4)/2a
Working this out, we get that a = 2/3. So statement (ii) is false, ruling out answer choices (B) and (C). What remains is to figure out whether statement (I) must be true.
Let’s see what we’ve pinned down: we know the x-location of the vertex, and the value of a. What’s at stake for statement (1) is the value of c, a simple constant term that adds to/subtracts from the overall y-value. Thinking about this visually, changing the value of c just slides the parabola up and down, leaving its shape and horizontal position unaltered.
But we’ve been told something else important: k, the y-coordinate of the vertex, is negative. What does this mean for the value of c?
To investigate this, my move would be to figure out the equation for where k exactly equals 0. This may seem perverse, since we’ve been told k is strictly less than 0. But examining what’s going on at the boundary is often very informative!
So, now to more flexible putting-together of different ways of thinking about quadratics. If k = 0, the parabola just grazes the x-axis; this means it has a double root. But we know the a-value and the x-coordinate of the root, so we can write the equation down for this case:
y = a(x – r)2
y = (2/3)(x – (-3))2
The constant term here works out to be 6. But that’s just c! Now, we know this is not an allowed position of the curve; the vertex’s y-coordinate is strictly below 0, not = 0 as here. But logically, we can get as close to c = 6 as we like, so clearly c doesn’t have to be negative. It could be, but that’s not what we need to evaluate (rather, whether it must be).
Whew! After all that, we’ve found our answer: (D), neither (I) nor (II) must be true.
That was… ugly, and time-consuming. What else can we do? This problem yields easily to Desmos, if you know what you’re doing. We’ll enter in the equation and use sliders for a and c (Desmos prompts you with this possibility when you type them in).
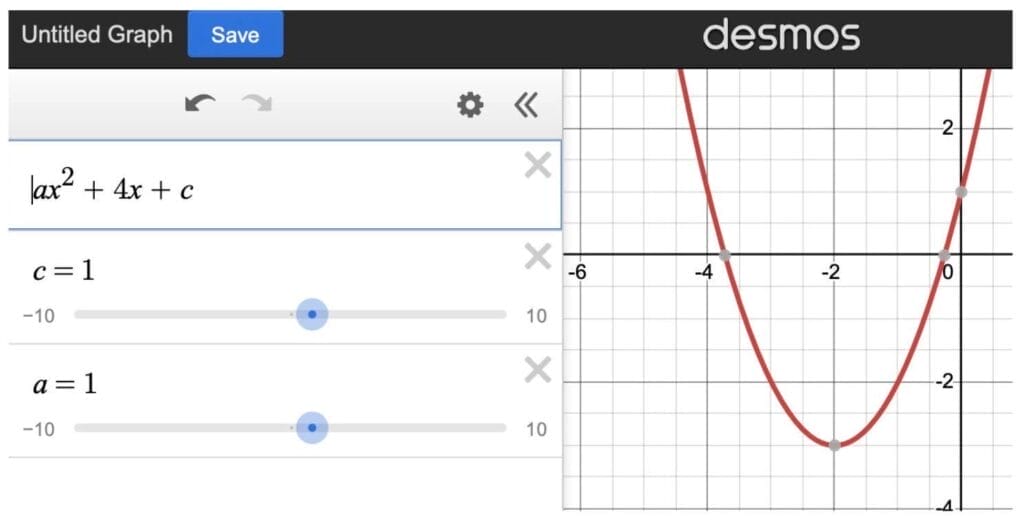
From here, simply move the sliders and see what happens! You’ll discover that changing c shifts the parabola up and down without otherwise transforming it:

Meanwhile, changing moves the parabola left and right (and eventually flips it over).
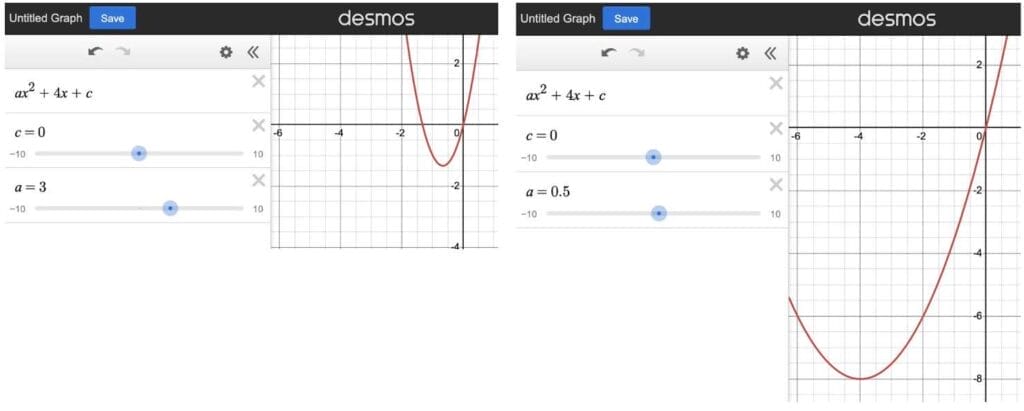
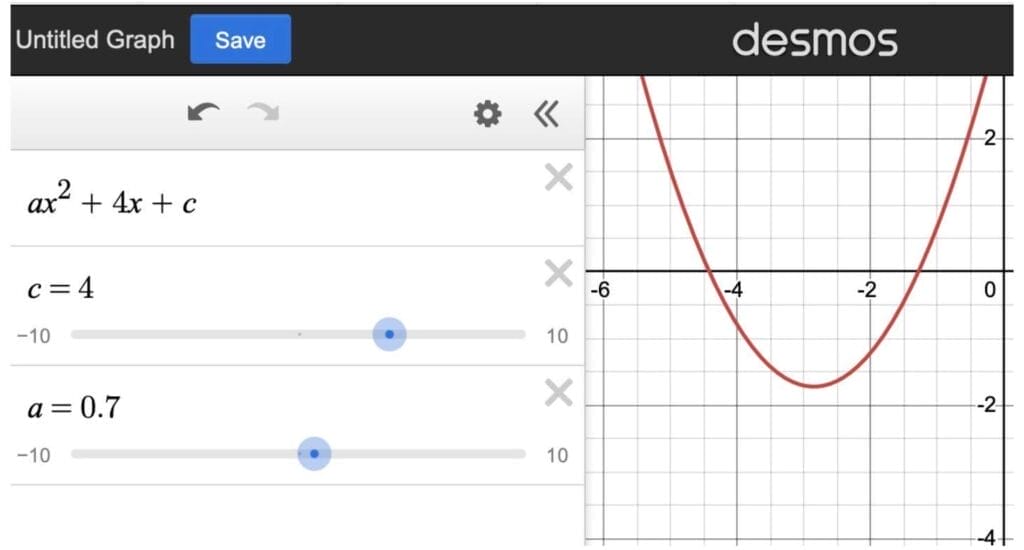
Seeing this, we adjust a until the vertex lands on x = –3 (see above for the reasoning); it looks close to 0.7.
Going further, what we have on screen has a vertex with a negative y-coordinate, as required, while c = 4. So, it’s safe to say c doesn’t have to be negative.
Assuming you’re still with us, let’s have another one…
How to Tackle the Most Difficult Digital SAT Math Questions: Example 2

As typical with math problems, there are several ways through this. If you know the basics of calculus, this problem is fairly trivial: it amounts to asking where the quadratic curve has a slope of 3 (equal to the slope of the line — this must be where the line and parabola touch). The slope at any point on the curve is just the first derivative, which for this parabola is 4x – 21. Setting that equal to 3, we get x = 6, so the answer is (C). Problem solved!
Of course, the SAT doesn’t assume you know calculus, and you don’t need it to solve this problem. What else could we do? Understanding that we’re looking for where the two curves intersect, we could try setting them equal to each other, getting an equation with just x (…and a):
2x2 – 21x + 64 = 3x + a
And we can do some algebra to manipulate this, bringing the x terms together.
2x2 – 21x + 64 = 3x + a
– 3x – 3x
2x2 – 24x + 64 = a
– 64 – 64
2x2 – 24x = a – 64
At this point, there are a few ways forward. One option is realizing that we still have a quadratic equation and want it to have a unique solution. We could then write an equation for the determinant (setting it equal to zero gives us a unique solution). We would solve first for a value for a, then get the x-value.
Instead, we’ll illustrate another solution path, involving completing the square. We’ll divide both sides by 2 first to make the left side prettier:
x2 – 12x = a/2 – 32
x2 – 12x = a/2 – 32
x2 – 12x + 36 = a/2 – 32 + 36
(x – 6)2 = a/2 – 4
Taking square roots, being careful to allow for negative values:
x – 6 = ±√(a/2 – 4)
x = 6 ± √(a/2 – 4)
Now we need to engage a bit of logic. Recall that we’re trying to find a unique point of intersection. In the equation we derived above, a could be anything, and we could get no solutions (line doesn’t touch parabola), or two solutions — two x-values where the line crosses the parabola. To get a unique point of intersection, we should get a unique x-value… so what we’re adding and subtracting must be reduced to 0. That makes x = 6. (Notice that we didn’t actually bother to figure out the value of a.)
If all of that seems… horrible… don’t despair! There’s yet another way in, and one that’s much more approachable.
An indispensable tool available to you for the digital SAT is the Desmos calculator, and it’s really helpful here. In fact, just graphing the quadratic equation alone is probably enough to answer this question.
I’ve just entered the first equation into the online version of Desmos.
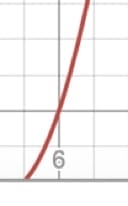
Take a closer look around the points where x = 6 and x = 8, the only two answer choices in contention.
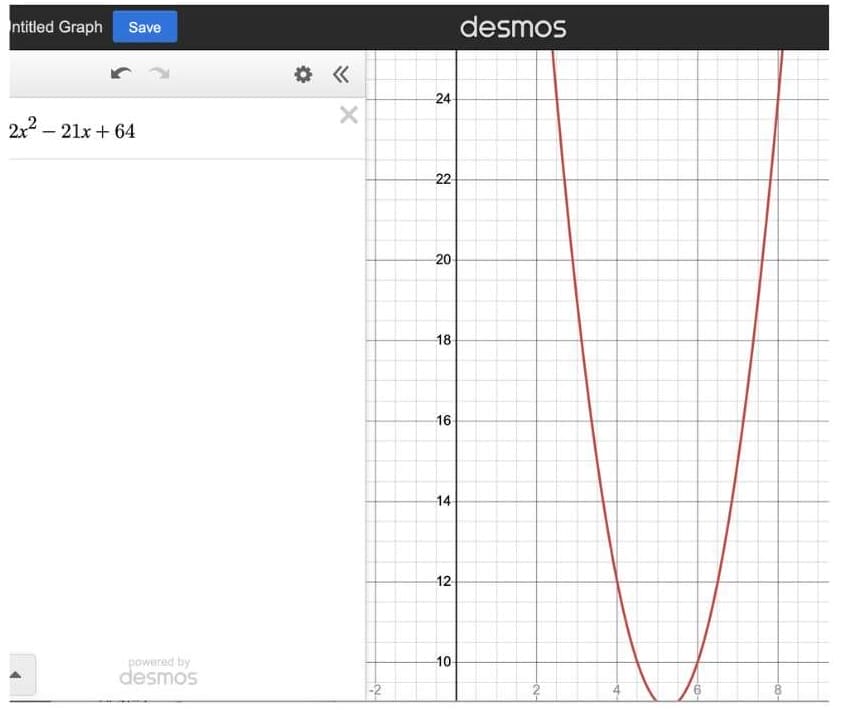
It’s extremely steep at x = 8, while near x = 6 the slope looks to be right around 3 (up three boxes, over one…). Just seeing this, I’d be confident marking (C).
But there’s more we can do with Desmos to really be sure here. Let’s enter the line equation, and use the slider function (Desmos suggests this automatically for variable a).
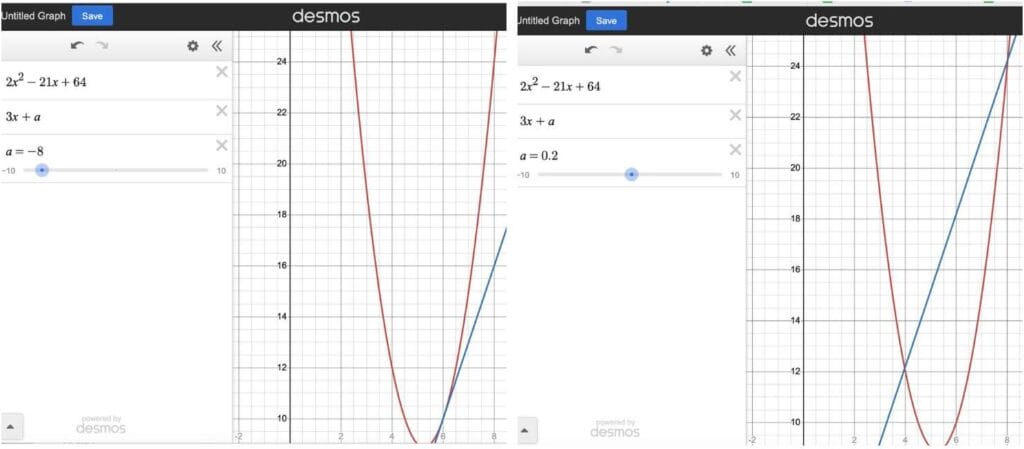
Adjusting the slider to make the line hit the curve at either x = 6 (left) or 8 (right), now we can be sure that (C) is the right answer.
So… is the lesson that you should use Desmos for everything? Or at least for the hardest problems? Not necessarily.

How to Tackle the Most Difficult Digital SAT Math Questions: Example 3
One of the most important skills, in facing a problem like this, is keeping your cool and taking some time to assess the situation before getting into too much math. Among the things you should notice, and think about, is the spread among the answer choices. Here, it turns out to be huge: estimating, the answers are about 14, about 20, about 140, about 170. That’s a big spread! Maybe we don’t need to get our hands dirty with exact math; rough estimation will get us there.
Point A, on the circle, is about 1 unit by 10 units away from the center; the radius of the circle is just a little over ten, then. ACB is a right angle, so AB should be the hypotenuse of an isosceles right triangle with two radii as legs. (It’s a really good idea to draw it out, if you’re having any trouble visualizing it!) If they’re about 10 long, AB is about 14. So, the answer is (A); the others aren’t close — B is about a full diameter of the circle, already too long, and the other two are crazy out-of-bounds.
Of course, this problem can be done analytically, with repeated application of the Pythagorean theorem. It’s not wrong. or bad, to solve it that way. But it does take longer; if you come in ready to notice easier ways through a problem, you’ve got an edge.
How to Tackle the Most Difficult Digital SAT Math Questions: Example 4
And now, a real doozy.

This is, to say the least, opaque at first. Let’s dig in and see what we can make of it.
First, them telling us the coordinates of the vertex is huge. We can plug that into the vertex form of the equation:
y = a(x – h)2 + k (h, k) = vertex
y = a(x – 9)2 + -14 (9, -14) = vertex
y = a(x2 – 18x + 81) – 14
Now, let’s group things into standard form y = ax2 + bx + c
y = ax2 + bx + c
y = ax2 –18ax + 81a – 14
This still looks pretty ugly. But we are being asked about the sum of all the coefficients, so let’s grab those and see what we get:
a – 18a + 81a – 14
64a –14
Aha! Ok, now we’re in business. Recall that we’re told the parabola intersects the x-axis at two points, Since its vertex is below the x-axis, it must open upward, meaning a > 0, and thus, so is 64a. So, we have something positive added to negative 14:
(+) – 14
So… the sum of the coefficients must be greater than –14: (D) is the only answer that works.
Is this problem doable with Desmos? You’ll still need to know the vertex form of the equation, but if you do, you can put it into Desmos and explore its behavior using the slider function. You’ll quickly see that a = 0 is the critical point; bigger than that, the parabola intersects the x-axis; below, it doesn’t.

From here, you’ll still need to follow the same chain of reasoning above about the sum of the coefficients; it’s not clear that using the graphing calculator is much help here, and it may ultimately be a waste of time.
Summary
Let’s recap. We’ve walked through a number of the hardest Math problems from the Blue Book practice tests for the Digital SAT. We’ve highlighted the fact that quadratics are a favorite topic for these hardest questions and reviewed some of the essential knowledge and skills to navigate them successfully. Knowing how to use the tools in the Desmos calculator is important, but not sufficient; you’ll also want to have in hand a range of analytical techniques and strategic approaches. Above all, you’ll want to keep your wits about you, avoid panic, and be scrappy and flexible.

