At Reason Test Prep, we emphasize that problem solving gets easier when we can make things more concrete and tangible rather than abstract. People are better — faster, more accurate, and more confident — at reasoning about things they’re familiar with. So if we can find ways to translate abstract problems into concrete terms, we can make them easier to deal with.
Today, we’re going to apply this to polynomial long division, one of the more obscure algebra topics appearing on the SAT (and, less frequently, the ACT). At first glance, long division of polynomials can seem intimidating: either you remember that lesson from your algebra class, or you’re out of luck… right?
Let’s look at an example:

Before getting into the weeds with this one, we’re going to take a quick diversion into much more familiar territory. As exotic and ugly as polynomials may look, it turns out that there is a polynomial system we all know and use every day: the Arabic numeral system. For example, a number like 2,316 is really a sum of different powers of ten: 2 thousands, 3 hundreds, 1 ten, and 6 ones:
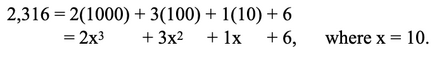
And once we look at things this way, it’s reassuring to discover that long division of polynomials works just like long division of the numbers we’re already familiar with. In fact, it’s even more straightforward: we don’t have to worry about the messy business of borrowing and carrying over between digit places. (On the other hand, the individual “digits” we’ll get aren’t limited to 0-9; they can be larger than 10, or even negative… more on that in a minute).
The actual division process is pretty simple. At each step, we just write down what we need to multiply the leading term of the divisor by to match the leading term of what’s left of the polynomial being divided. In other words, if we’re dividing by something that starts with 2×3… and we’re trying to match 6x5…, the next term in the quotient will be 3×2, because 2×3 * 3×2 = 6×5. Then multiply the whole divisor by this, and subtract from the polynomial you’re dividing. The leading term will cancel, and you’ll be left dividing a polynomial of lower degree; rinse and repeat. If we end up with 0 at the last step, great: that means the divisor divides the polynomial. If there’s some other number R there, that’s the remainder and will appear in the result as R/D, where D is the polynomial you were dividing by.
Okay, that got pretty abstract. Let’s take our own advice and make this concrete by looking at our earlier example. We’ll do 2x3 + 3x2 + x + 6 ÷ x + 2, side-by-side with the equivalent regular long division 2316 ÷ 12, expressed a little weirdly with explicit powers of ten.
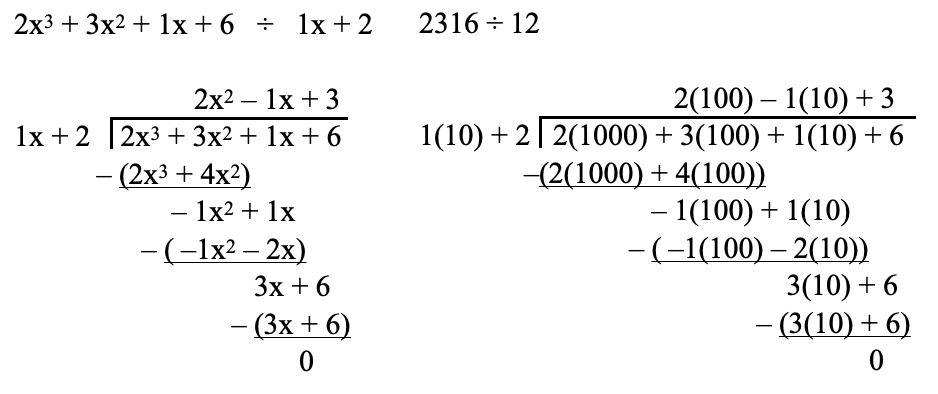
Either way, we get 2x2 – 1x + 3 = 2(100) -1(10) + 3 = 193, which is indeed the right result for 2316 ÷ 12. This may look a little weird, because we have a negative tens digit, but this is what we need to do if we can’t exploit the known value of the variable to allow “borrowing”.
In fact, thinking about it, negative digits are also familiar from another well-known number system: the Roman numerals! In the Roman numeral system, X represents 10, I represents 1… but written with the I in front of the X, it’s a negative digit: IX = 10 – 1 = 9. Let’s push this parallelism between polynomials and Arabic numerals just a little further to illustrate a common pitfall. Suppose we were given the following division problem:
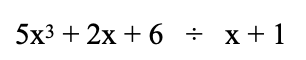
Setting it up without thinking too much about it:

Something went wrong here. We correctly cancel out the leading term, but in the second term we’re trying to subtract an x2 thing from an x thing… that’s not right.
Here again, thinking about the polynomial system we already know (Arabic numerals) rescues us from our confusion. The equivalent numeric division would be:
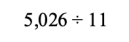
Aha! We missed out the necessary x2 term with a 0 coefficient (we have to write it as 5x3 + 0x2 + 2x1 + 6 to do the division properly). Put another way, we wrote it down as if we were doing 526 ÷ 11, which is clearly not the same problem.
This post has gotten deeper into the weeds of mathematical content than usual. But it serves well, we think, to illustrate something really important. To reiterate, finding ways to understand abstract mathematical expressions in more tangible and familiar terms makes them much easier to think about. What looks at first like a hard, exotic kind of problem turns out to be pretty easy to deal with, once we see how to leverage what we already know.

