Many of you may be aware of the book The Black Swan by Nassim Nicholas Taleb. In the book Taleb uses the analogy of a black swan in nature to describe the problem of predicting highly improbable events. He comments that just because one has never seen a black swan in nature doesn’t mean that it does not exist (and he ties this analogy to the folly of predicting events in the markets based on past events). In this article I will to tie this concept to Data Sufficiency and they way (and certainty with which) we draw conclusions about the statements.
Different Data Sufficiency questions call for different approaches, but there are some for which picking numbers is either the best or the only viable option. On these questions the idea is to pick numbers to see whether only one answer to the question is possible or whether multiple answers are achievable. The best-case scenario, from a test takers perspective, is when you can prove that more than one answer is possible. In that situation you know that the statement is not sufficient and if you have really tested cases to prove that 2 answers are possible, then you know 100% that the statement is not sufficient. Case closed.
But what happens when you have tried a couple of numbers or sets of numbers and you keep getting the same answer? This is where test takers often go wrong. Often people will conclude that because they got the same answer in 2 or 3 situations, they will always get the same answer. This is the Black Swan of Data Sufficiency – concluding that because you have never seen a black swan (or, in this case, a different answer to the question) one does not exist.
This is the kind of unwarranted assumption that the writers of the GMAT want you to make and they often design data sufficiency questions to draw you into making one. And I think this gets at the relevance of Data Sufficiency – most people bemoan DS questions and the GMAT more generally, but a person who is going to prematurely conclude that there is only one answer to a DS question is likely to be the same person who will erroneously conclude that some event in the financial or business world will never happen.
So how does one avoid drawing such a premature and potentially unwarranted conclusion? Well there are a few ways. Most test prep companies teach students to make sure they pick special kinds of numbers in these situations, numbers like 0, 1, negative numbers, fractions, etc. And that is generally good advice. Those are often the kinds of numbers that will produce a different result when more common numbers (like 2 or 3) might continue to produce the same result.
But on harder questions what is really needed is some good, old-fashioned quantitative reasoning. The mistake that people often make is to pick numbers without applying any thought to why certain numbers are producing a certain result and what numbers might be used in order to get a different result. Instead they sort of uncritically lob some numbers in (or even worse “pre-select” the numbers they will use instead of choosing the second number based on what they saw happen with the first) and then get the question wrong. The key is to think conceptually about what is happening and why, or at the very least pay attention to the pattern of what is resulting each time you pick a number and try to adjust accordingly. The below question is a very difficult one, but it helps illustrate this point:
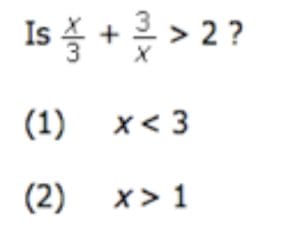
On statement 1, most people start picking numbers like 1 or 2 and see that you get a yes answer to the question and then think to pick negative numbers and see that in those cases you will get a no answer. So, not sufficient.
Statement 2 is a little harder. Most people will again pick a number like 2 (which, again, will produce a yes answer) but then often pick numbers like 5 or 10, which likewise produce a yes answer. At that point most people will erroneously conclude that because they have gotten the same answer on 2 or 3 tries, it MUST BE sufficient. This is the Black Swan of Data Sufficiency!!! It obviously could be the case that the statement is sufficient, but can we really conclude that because we have gotten a yes answer 2 or 3 times the answer will ALWAYS be yes? To do really well on Data Sufficiency you want to try to arrive at answers with as high a level of certainty as possible…and it’s not that you want to try a million numbers here. It’s more that you want to think about why the numbers you are choosing are producing that result or look at the pattern of what results from the numbers you choose to see if you can infer what types of numbers might lead to the result that you want.
So on this question, the first and most obvious thing to do is just look at the original equation in the question stem and consider that because you have 3 in the numerator and denominator of the two fractions 3 would probably be a good number to select! Doing so will produce a 2, which is not bigger than 2, so the answer would then be no!
But another thing that you can do here (and on other hard data sufficiency questions) is to pay attention to the pattern of what is outputted for every input that you select. When x = 1, the output is just over 3. When x =2, the output is just over 2. (You don’t even need to fully calculate these to see this – just some quick estimation will do.) So the output is starting to near 2. Now, if you start trying numbers like 5 or 10, you will see that the output starts to climb away from 2 and that the larger the value of x, the larger the output. So clearly large values of x are not going to get the expression to be less than or equal to 2. But why did the output dip down from 1 to 2 and then start to climb back up at a certain point? Where will the output bottom out? Here again, it helps to just look at the expression and guess that 3 might be a special case. But if the output dips down as you approach 3 and then climbs back up as you go to 4 or 5 or 10, then obviously it makes sense to try 3.
This is the kind of quantitative reasoning that the GMAT rewards. It’s certainly not easy, but it beats the sort of uncritical acceptance of the idea, “well, I tried 2 sets of numbers and got the same result, so the result must always be the same!” Again, that is the Black Swan of Data Sufficiency and some questions are designed to punish that kind of thinking. And with good reason. If you are going to draw those kinds of conclusions on the GMAT then maybe you will erroneously draw them in the real world too! Don’t do it!
To finish up with the above question, we now know that the statements are not sufficient individually. Taking them together, obviously the 2 things that allowed the expression to not be bigger than 2 (negative numbers and 3) are now no longer options. X must be between 1 and 3. At this point, you really need to apply the same kind of reasoning as above. When x = 1, the output is over 3. When x = 2, the output gets lower and is just over 2. When x = 3, the output equals 2, and then with values of x that are greater than 3, the output climbs back bigger than 2. So just with that alone, it would appear that the expression bottoms out at x = 3 and that with any values of x between 1 and 3, the output will be bigger than 2.
Do we know this to be the case? No. It’s possible that at x = 2.999 the output will be less than 2. So again we can’t conclude that because we have not see the black swan it does not exist. But in this case we have applied some pretty thorough reasoning and seen the pattern of what is happening, so it is very, very unlikely that there will be a value of x between 1 and 3 that will produce an output less than or equal to 2. And in the context of the time pressures of the test, it would be worthwhile to move on once we reach this kind of level of certainty. And indeed the correct answer is C.
Remember, the GMAT is a reasoning test – it tests quantitative and verbal reasoning. What the questions are designed to do is test your logical reasoning ability. Sure it helps a lot to have good foundational quantitative and verbal skills, but that is really just a foundation. Many questions are designed to punish people for leaning too much on that foundation and reward those who problem-solve creatively and think critically about the questions they face. So be careful about the conclusions you draw on Data Sufficiency and if you find yourself in a situation where you are picking numbers on a Data Sufficiency question, try to reason as you pick and think critically about the numbers you are picking and why you are picking them. And beware of the Black Swan of Data Sufficiency!

